本篇是当我们的模型或者算法表现的不好的时候,应该如何去调试问题,优化算法,调整数据,优化模型。
Orthogonalization
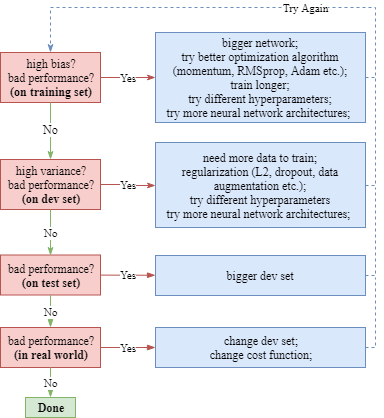
机器学习的模型训练过程依次有四个阶段:
- 在训练集上模型对损失函数拟合的好 如果不的话,我们可以调整神经网络的规模、或者调整最优化算法。
- 在验证集上模型对损失函数拟合的好 如果不的话,我们可以扩大训练集,或者尝试正则化方法。
- 在测试集上模型对损失函数拟合的好 如果不的话,我们可以尝试扩大验证集。
- 在生产环境上模型对损失函数拟合的好 如果不的话,我们可以调整数据集的设计,或者调整损失函数的设计。
我们假设上面这个阶段的问题的解决方法是互不影响的,也就是正交的。 Orthogonalization 正交的意思是,我们希望每种调整方式只会影响一个阶段,而不会对其他阶段产生影响,以免把问题复杂化。
诊断手段
数据集检查
Tensorboard观察loss变化
试试梯度检验
梯度检验是在编写机器学习算法时必备的技术,可以检验所编写的cost函数是否正确。
是否存在 train eval skew
如果用于训练的数据和生产环境的输入数据的分布不同,或者如果训练得到的模型部署到到生产环境后会有差异,都会产生训练-预测倾斜。
样本集有问题
数据集分布不同
如果需要处理的实际数据的分布和开发集/测试集数据的分布情况不同,那么算法不可能表现的足够好。
DownSampling 是要删除某一些样本,以减弱一些信号。
UpSampling 是要插入一些样本,以加强一些信号。
训练测试样本集中有错误数据
比如label错误率或者feature错误率。自然会影响到模型误差。
训练方法有问题
怎么判断训练出的模型是否拟合的比较理想? 数据集下的预测结果
模型结构有问题
训练目标选的不好
评价指标选择的不好
没有做误差分析
误差分析(Error Analysis) 指的是检查被算法误分类的开发集样本的过程,以便帮助你找到造成这些误差的原因。
学习算法的预测误差, 或者说泛化误差(generalization error)可以分解为三个部分: 偏差(bias), 方差(variance) ,噪声(noise).
偏差和方差是误差的两大来源。总误差=偏差+方差。
-
算法的偏差(bias):算法在训练集上的错误率。它意味着训练的模型在训练集上的拟合程度。
-
算法的方差(variance):算法在开发集(或测试集)上的表现比训练集上差多少。它意味着训练的模型在新数据上的表现。
减小算法的偏差,就需要提高算法在训练集上的性能。
减小算法的方差,就需要优化模型的泛化能力。
通过手动检查约 100 个被算法错误分类的开发集样本来执行误差分析,并计算主要的错误 类别。使用这些信息来确定优先修正哪种类型的错误。
一般的方法是:在每一个epoch计模型在train set上的loss和在test set上的loss,通过比较两者的走势来判断当前的误差主要源于哪一种。
算法在开发集上过拟合或欠拟合
- 偏差低,方差却高。 意味着过拟合。
如果你发现算法在开发集上的性能比测试集好得多,则表明你很有可能在开发集上过拟合了。在这种情况下,你需要获取一个新的开发集。
可以尝试增大训练集的数据量。 可以尝试添加正则化方法。
- 偏差高,方差却低。意味着欠拟合。
如果模型在训练集和测试集上表现类似,都不怎么好,则表明可能没有拟合好训练集。
可以尝试加大模型的规模,比如增加深度、层数等。
- 偏差高,方差也高。
如果模型在训练集表现不好,在测试集上表现的更差,那么表明当前的模型确实很糟糕。
- 偏差低,方差也低。
这是我们最期望的状态。
存在数据泄露(特征穿越)
梯度消失问题(gradient vanishing problem)
现象:梯度消失问题发生时,接近于输出层的hidden layer 3的权值更新相对正常,但前面的hidden layer 1的权值更新会变得很慢,导致前面的层权值几乎不变,仍接近于初始化的权值,这就导致hidden layer 1相当于只是一个映射层,对所有的输入做了一个同一映射,这是此深层网络的学习就等价于只有后几层的浅层网络的学习了。
原因:当链式求导,层数越多的时候,求导结果会越小。
解决方法:考虑用ReLU激活函数取代sigmoid激活函数。
梯度爆炸问题(gradient exploding problem)
现象:由于初始化权值过大,前面层会比后面层变化的更快,就会导致权值越来越大,梯度爆炸的现象就发生了。梯度更新将以指数形式增加。
原因:对激活函数进行求导,如果此部分大于1,那么层数增多的时候,最终的求出的梯度更新将以指数形式增加。
解决办法:考虑用ReLU激活函数取代sigmoid激活函数。
训练速度有问题
模型的规模和数据的规模增大之后,训练的速度可能成为瓶颈。
向量化
向量化(Vectorization)是一种能够消除代码中for循环的艺术,它能够极大的提升神经网络代码的训练速度。
尽可能多的使用向量运算,而不是手写for循环去运算。
参考
https://www.mlyearning.org/
NN参数调优 https://yangxudong.github.io/deep-learning/
https://medium.com/@jonathan_hui/debug-a-deep-learning-network-part-5-1123c20f960d
https://towardsdatascience.com/checklist-for-debugging-neural-networks-d8b2a9434f21