这几年深度神经网络在解决模式识别问题上有很大突破，比如计算机视觉、语音识别领域、语言翻译领域。

一般的回归预测问题常用标准神经网络模型(Standard NN，Feedforward NN)，图片分类问题常用卷积神经网络(CNN)，语音识别问题常用递归神经网络(RNN)。

深度学习的三位创始人Geoffrey Hinton, Yoshua Bengio, Yann LeCun, 因其在深度学习理论及工程领域上的重大贡献，获得了2018年的图灵奖。

多层感知机、玻尔兹曼机、受限玻尔兹曼机

多层感知机器(MLP)，是一种前向结构的人工神经网络，映射一组输入向量到一组输出向量。这是最简单形态的深度学习模型，全名Multi Layer Perceptron(MLP)，或是Deep Neural Network(DNN).

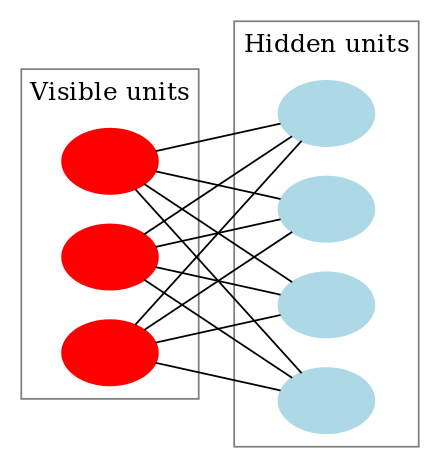
玻尔兹曼机的图像表示：每条无向边都表示一对依赖关系. 如图，在这个例子中有三个隐藏节点和四个可见节点。

受限玻尔兹曼机的图像表示:只有两层，没有输出层作为label。

如图，这个例子包含三个可见单元和四个隐单元。

为什么神经网络可以拟合任意的函数？

Universal approximation theorem(Hornik et al., 1989;Cybenko, 1989)定理表明：前馈神经网络，只需具备单层隐含层和有限个神经单元，就能以任意精度拟合任意复杂度的函数.

神经网络的构成

这是一个演示神经网络工作的WEB界面，通过它可以了解到神经网络的基本构成和工作流程。

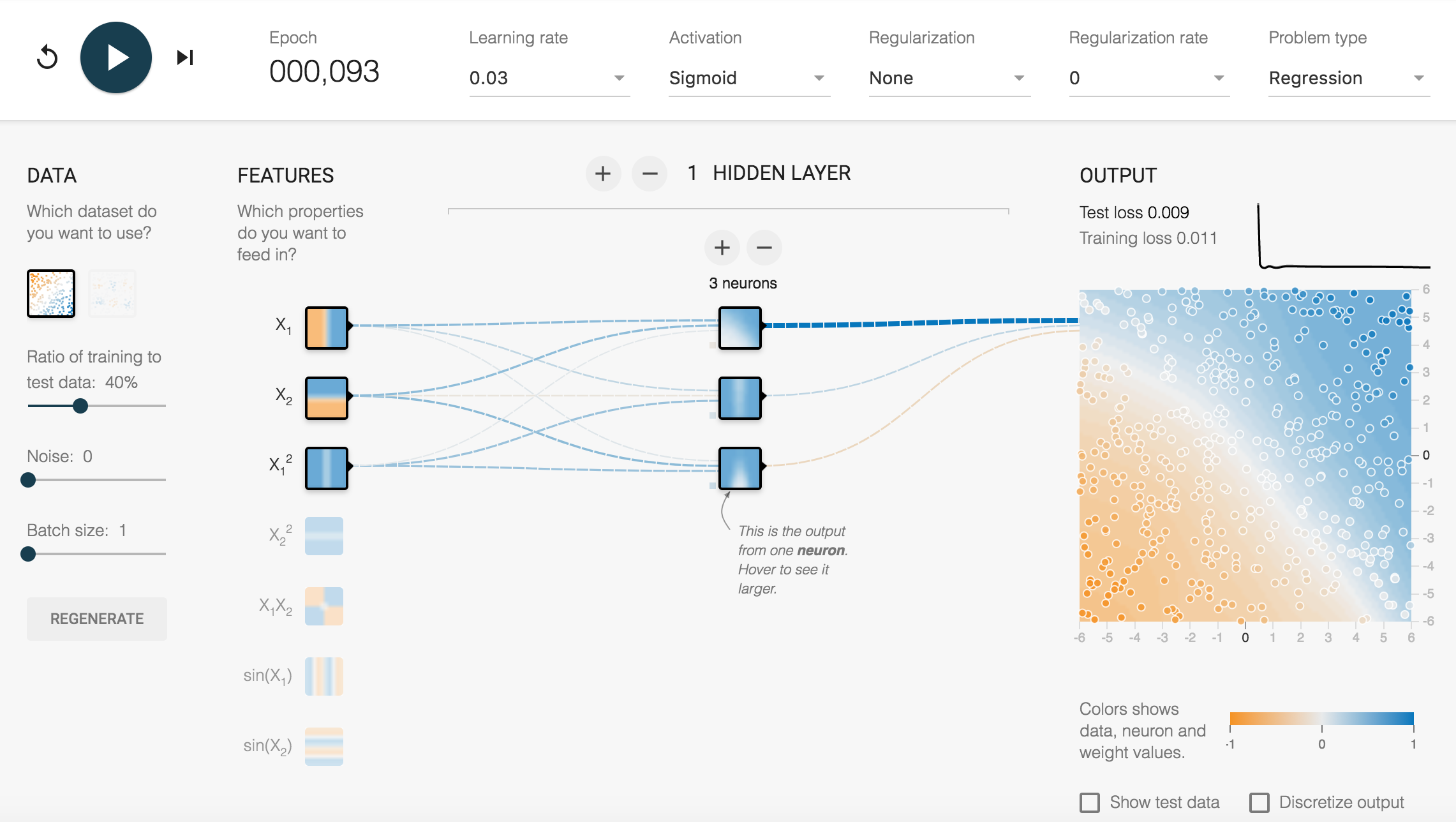
NN-playground

NN模型的核心元素

神经元 Neuron

Neuron是神经网络的一个单元。它是一个函数，一个回归模型。

那么机器学习的关键就在于，怎么根据数据来训练模型，也就是怎么根据样本数据来找到最合适的模型参数。

隐含层 Hidden Layers

神经网络是一层一层组织起来的。每一层由一个或多个Neuron组成。

通常一个神经网络，其隐含层层数、每层的Neuron个数，都是不一定的。对于最最简单的神经网络，可以没有隐含层，那么就只有输入层和输出层，输出层有唯一一个神经元。

输出数据

如果是分类问题，那么数据就是离散的值。如果是回归问题，那么数据就是连续的值。

NN模型的数据和特征 Features of data

把真实世界的对象抽象出矩阵形式的数据，尤其是要把对结果有影响的数据以一定的数学表达抽象出来。比如图像、比如声音、比如语言。

相对于其他类型的模型，NN模型对输入的要求更加宽容。但依然免不了特征工程中从“raw data” 到向量的处理过程，毕竟计算机的一切都是0101化的。越来越多的端到端模型把数据预处理、特征表示、向量化的过程纳入到模型内部。

NN模型的参数初始化

尽可能小的参数初始值

Xavier 初始化 Xavier初始化方法是一种很有效的神经网络初始化方法，目标就是使得每一层输出的方差应该尽量相等。

NN模型的代价函数 Cost Function / 损失函数 Loss / 误差函数 Error / Objective 目标函数

cost function 用于表示所训练出模型的好坏程度。它是构建一个网络模型必须的两个参数之一。

任何能够衡量模型预测出来的值 h(θ) 与真实值 y 之间的差异的函数都可以叫做代价函数 C(θ)。

比如cost function返回一个非负数，这个数会表示神经网络将训练样本映射到正确输出的准确率。cost返回值越小表明训练结果越好，那么模型训练的过程就是在使得cost尽可能小的过程。

一个好的代价函数需要满足两个最基本的要求：能够评价模型的准确性，对参数θ可微。

下面有几种常见的代价函数。

交叉熵 cross-entropy Loss

交叉熵损失函数简单来说就是样本的预测概率和真实概率的乘积。

Loss = -actual * (log(pred)) - (1-actual)(log(1-pred))

对数损失函数向多类别分类问题进行的一种泛化。交叉熵可以量化两种概率分布之间的差异。

交叉熵损失(Cross-entropy Loss)，也叫对数损失（Log Loss），其本质就是最大似然估计（最小化对数似然的负数，相当于最大化似然函数）。

均方误差 Mean Square Error Loss

K-L散度 Loss

NN模型的优化方法

另一篇文章有单独去介绍最优化方法

训练神经网络的目标是找到使最小化损失函数的神经元权重组合。

优化方法指的是不断更新网络的参数，使得它能显著地降低代价函数。优化器是编译网络模型必要的两个参数之一。

激活函数 Activation Function

激活函数是在神经网络的某些层运算中加入非线性转换。使其能够学习更复杂的函数。如果没有它, 神经网络将只能够学习线性函数, 它只能产生输入数据的线性组合。

计算输入数据的带权之和，加上一个偏差，然后判断该样本的结果（是否“激活”）。

激活函数可以通过设置单独的激活层实现，也可以在构造层对象时通过传递activation参数实现。

常见的激活函数：

Sigmoid Function

Sigmoid函数也称为logistic函数, 它是连续的, 也容易计算导数。它将所有的实数压缩到范围 0到1之间。

A = 1/(1+e^(-x)

输出范围0-1之间。

Tanh Function

A = 2/(1+e^(-2x)) - 1 = 2sigmoid(2x) - 1

输出范围是-1，1之间。

SoftMax

Softmax 是一个泛化的Sigmoid函数，当我们要处理多个类。所有输出值都在范围 (0, 1) ，其总和为 1, 因此可以将输出解释为概率。它称作是归一化指数函数。

ReLu function 线性整流函数

ReLU 函数如果输入小于或等于 0,则输出0 否则输出输入的值, 我们可以把它们看成开关。它可以免受梯度消失的问题, 它计算非常快。在卷积网络中的应用时比应用Sigmoid函数更有效。

通常意义下，线性整流函数代指代数学中的斜坡函数，即 A = x if x>0 else 0

其中ReLu应用的最多，可见 https://www.cnblogs.com/alexanderkun/p/6918029.html

Dying ReLU: Relu有一个缺陷是，当梯度值过大时,权重更新后为负数,经relu后变为0,导致后面也不再更新. 为解决这个问题，出现了Leaky Relu，当输入为负数时，返回一个大于0的小值。

模型评估 Evaluation

每次轮计算后评估模型的方法。需要一个指标。

机器学习模型的评价方法和指标

前向传播forward pass(FP)、后向传播backward pass(BP)

正向传播比较直观，就是把一个测试数据放入当前的模型（可能还没训练完成，参数也许还是随机值），经过模型的计算，得到一个输出。这就是一次正向传播。

反向传播的目的是要用这一次正向传播的结果来更新参数。首先列出误差（正常传播结果与样本结果的误差），计算误差对某个参数的偏导函数。那么该参数的新值就更新为原值 - 更新速率 * 偏导数。

””” 不是任意的模型结构都可以通过反向传播来更新参数。反向传播是一种特定的算法，它适用于那些满足以下条件的神经网络模型：

可微分性（Differentiability）: 反向传播依赖于模型的参数是可微分的。这意味着模型的每一层以及损失函数都必须是可微分的，以便计算梯度。如果模型包含不可微分的操作或者结构，那么传统的反向传播算法就无法直接应用。
链式结构（Chain Structure）: 反向传播利用链式法则来计算梯度。这要求模型可以表示为一系列函数的组合，其中每个函数的输入依赖于前一个函数的输出。如果模型结构不支持这种链式分解，那么标准的反向传播就不适用。
固定结构（Fixed Architecture）: 反向传播通常用于固定结构的网络，即网络的层数和每层的结构在训练前就已经定义好。对于动态变化的结构，例如树形结构的神经网络或者递归神经网络，在某些情况下可能需要特殊的反向传播变种或者其他技术。
有明确定义的损失函数（Well-defined Loss Function）: 必须有一个明确的损失函数来衡量模型输出和目标之间的差异。这个损失函数应该是关于模型参数的函数，以便通过梯度下降方法优化这些参数。

如果模型结构不满足这些条件，那么可能需要使用其他类型的优化算法。例如，对于包含离散操作的模型，可能需要使用强化学习或者进化算法；对于非固定或自适应结构的模型，可能需要使用基于梯度的方法的变体或者完全不同的方法。

此外，即使模型结构理论上支持反向传播，实际上也可能由于计算资源的限制（如内存容量）而无法实施。在这种情况下，可能需要使用梯度累积、模型剪枝、量化或其他优化技术来适应资源限制。 “””

以下是一些可能不支持标准反向传播的模型结构示例：

1. **含有离散操作的模型**:
   某些模型可能包含离散决策步骤，比如基于特定规则的决策树或者使用离散激活函数的神经网络。由于离散操作不是连续可微的，传统的反向传播无法直接用于这些模型。例如，如果一个神经网络层使用了阶跃函数作为激活函数，这个函数在大部分地方的导数为零，这就无法通过反向传播有效地计算梯度。

2. **含有随机性的模型**:
   某些模型可能包含随机性，比如随机神经网络（Stochastic Neural Networks）或者使用了随机采样步骤的模型。虽然存在针对这类模型的反向传播变体，如随机反向传播（Stochastic Backpropagation），但标准的反向传播算法可能不适用。

3. **神经图灵机（Neural Turing Machines, NTM）**:
   神经图灵机和其他一些内存增强网络可能包含复杂的读写操作和内存访问机制，这些机制通常不是直接可微的。尽管有方法可以训练这些模型，但它们可能需要特殊的优化技术。

4. **神经网络的变分结构**:
   一些模型的结构在训练过程中是可变的，比如神经架构搜索（Neural Architecture Search, NAS）中动态变化的网络结构。这些模型的结构和参数同时进行优化，可能需要特殊的算法来处理结构的变化。

5. **基于进化算法的模型**:
   进化算法（如遗传算法）通常用于优化模型的结构和参数，而不是优化单一的参数集。在这些情况下，模型的更新不是通过反向传播进行的，而是通过模拟自然选择的过程。

6. **量子神经网络**:
   量子计算中的量子神经网络利用量子比特进行操作，这些操作不符合传统神经网络的可微分性要求。虽然有量子版本的反向传播算法，但它们与经典的反向传播算法有显著不同。

训练迭代的超参数

超参数相对于模型参数不能从数据中学习, 它们是在训练阶段之前设置的。

Iteration

iteration表示1次迭代（也叫training step），每次迭代更新1次网络结构的参数.

Iterations is the number of batches needed to complete one epoch.

每一个pass（正向 + 反向）使用 Batch size 个样本。

Epoch

Epoch 是对所有训练数据（注意这里指的是all train data）的一轮 forward pass 和 backward pass过程。

The number of epochs is the number of complete passes through the training dataset.

One Epoch is when an ENTIRE dataset is passed forward and backward through the neural network only ONCE.

An epoch is comprised of one or more batches.

可根据实际问题来定义epoch，例如定义10000次迭代为1个epoch，若每次迭代的batch-size设为256，那么1个epoch相当于过了2560000个训练样本。

我觉得epoch可以理解为generation.

Batch

Batch size 是要一次通过神经网络的样本个数。指每个小批量的样本数。

计算一次loss，利用这次loss更新网络权值，这就是度过了一次batch。

The batch size is a number of samples processed before the model is updated.

下面是一个不使用和使用Batch来训练的例子对比

Num Step

num_steps为每个样本所包含的时间步数。表示一起训练多少时间步，又叫做seq_len.

该参数常见于时序数据，比如NLP语料。num_step是每个切片的 token 数，即序列的长度 seq_len。

Learning Rate

Learning rate 用于控制每次更新参数时参数变化的程度。表示更新参数的快慢程度。

正规化 Regularization method

Regularization 的目的是要避免过拟合。减少真实数据生成错误（不是样本数据训练错误），避免训练数据过于片面，避免模型过于贴合训练样本而不能反映数据的真实规律。

下面有四种Regularization方法，

Dataset augmentation

通过已有的数据集来构造新的数据，如果手里现有的样本数据不够充分、丰富，那么我们就自己人造出丰富、充分、合理的数据。

Early stopping

在训练损失仍可以继续减少之前结束模型训练。使用早停法时，我们会在基于验证数据集的损失开始增加（也就是泛化效果变差）时结束模型训练。迭代次数不是越多越好，我们可以在训练模型过拟合之前停止训练。随着迭代次数增多，训练错误率会越来越小，但测试错误率可能会反弹。这就是希望我们找到一个最小化测试错误的最佳时机。

Dropout layer

加入一层Dropout layer，在训练的时候，该层随机断开一些节点。在真正预测的时候，还是使用全部的连接。这是正则化的一种形式，在训练神经网络方面非常有用。丢弃正则化的运作机制是，在神经网络层的一个梯度步长中移除随机选择的固定数量的单元。丢弃的单元越多，正则化效果就越强。这类似于训练神经网络以模拟较小网络的指数级规模集成学习。

Dropout: A Simple Way to Prevent Neural Networks from Overfitting

以贝叶斯估计来看待Dropout

权值衰减 Weight penalty L1 and L2

Weight penalty基于一个假设：模型的权重越小，模型越简单，要尽量使得权重的绝对值小。

Weight penalty的方法有两种：L2和L1. 他们用于附加在cost function的计算上。

L2 正规化是附加权重的平方之和，L1是附加权重的绝对值之和。

归一化 Normalization

Normalization 的目的是为了加快训练效率（训练速度）。

Batch Normalization

BN由2015年提出，近年来越来越流行，几乎被用在每一种神经网络模型中，用于处理input layer。

Layer Normalization

RMS Normalization

RMSNorm的主要思想是根据特征的均方根（Root Mean Square）来进行归一化。对于每个样本，RMSNorm计算特征的均方根，并将特征值除以均方根来进行归一化。这样可以保留特征的相对比例，同时缩放特征的幅度，使其适合神经网络的训练。

网络分层

你需要了解：

某层的作用
某层的计算操作具体是怎么样的
某层应该放置在什么位置

全连接层 Fully Connected layer

也叫做 Dense 层。这是最普通的一种网络层。

所实现的运算是output = activation(dot(input, kernel)+bias)。其中activation是逐元素计算的激活函数，kernel是本层的权值矩阵，bias为偏置向量.

几个类似的术语

linear 线性层: 单个wx+b
dense 密集层：多个wx+b
FC 全连接层：多个wx+b
MLP ：得有激活函数

Activation层

激活层对一个层的输出施加激活函数。

Dropout层

这是为实现正则化而存在的层。上一节有介绍。为输入数据施加Dropout。Dropout将在训练过程中每次更新参数时按一定概率（rate）随机断开输入神经元，Dropout层用于防止过拟合。一般放置在输出层之前的一层。

注意这一层只能在训练的时候生效，在预测的时候就不要生效了。

Inverted dropout

Flatten层

Flatten层用来将输入“压平”，即把多维的输入一维化，常用在从卷积层到全连接层的过渡。Flatten不影响batch的大小。

Reshape层

Reshape层用来将输入调整数据维度转变为目标维度。

Permute层

Permute层将输入的维度按照给定模式进行重排，例如，当需要将RNN和CNN网络连接时，可能会用到该层。

Masking层

使用给定的值对输入的序列信号进行“屏蔽”，用以定位需要跳过的时间步

卷积层 Convolution layer

shared weights

局部连接层 Locally-connected Layers

卷积层其实只是局部权重共享的local connect.

池化层 Pooling Layer

池化层的操作是在从上一层传过来的参数矩阵中取一部分区域，然后继续传往下一层。常用的Pooling方法Max Pooling是取一小块区域中的最大值。

Recurrent层

Embedding层

我在另外一篇blog中单独介绍了Embedding的构建。 Embedding

Normalization层

BN(Batch Normalization)

训练深度网络的时候经常发生训练困难的问题，因为，每一次参数迭代更新后，上一层网络的输出数据经过这一层网络计算后，数据的分布会发生变化，为下一层网络的学习带来困难。 Internal Covariate Shift https://machinelearning.wtf/terms/internal-covariate-shift/ https://keras.io/zh/layers/normalization/ https://zhuanlan.zhihu.com/p/56225304 https://zhuanlan.zhihu.com/p/34879333

Batch Normalization的核心思想是对每个特征维度进行归一化。对于每个训练批次中的每个特征，Batch Normalization执行以下步骤：

计算该特征的均值和方差。
使用批次内的均值和方差对该特征进行归一化。
对归一化后的特征进行缩放和平移，以便模型可以学习适当的表示。

batchnorm层的放置位置很重要，可以尝试放在最输出层之前或embedding层之后。

Noise层

注入随机性

Merge Layers

将两条或者多条网络流合并。

Attention layer

这个层能帮助解码器聚焦于输入句子的相关部分（类似于 seq2seq 模型中的 Attention）。

attn_layer = AttentionLayer(name=’attention_layer’)([encoder_out,decoder_out])

def attention(queries, keys, keys_length):
  '''
    queries:     [B, H] 前面的B代表的是batch_size，取值为32，H是128，代表向量维度。代表的是预估item
    keys:        [B, T, H] T是一个batch中，当前特征最大的长度，每个样本代表一个样本的特征
    keys_length: [B]
  '''
  # H
  queries_hidden_units = queries.get_shape().as_list()[-1] #每个query词的隐藏层神经元是多少，也就是H
  # tf.tile为复制函数，1代表在B上保持一致，tf.shape(keys)[1] 代表在H上复制这么多次
  # 那么queries最终shape为(B, H*T)
  queries = tf.tile(queries, [1, tf.shape(keys)[1]])
  # queries.shape(B, T, H) 其中每个元素(T,H)代表T行H列，其中每个样本中，每一行的数据都是一样的
  queries = tf.reshape(queries, [-1, tf.shape(keys)[1], queries_hidden_units])
  # 下面4个变量的shape都是(B, T, H)，按照最后一个维度concat，所以shape是(B, T, H*4)
  # 在这块就将特征中的每个item和目标item连接在了一起
  din_all = tf.concat([queries, keys, queries-keys, queries*keys], axis=-1)
  # (B, T, 80)
  d_layer_1_all = tf.layers.dense(din_all, 80, activation=tf.nn.sigmoid, name='f1_att', reuse=tf.AUTO_REUSE)
  # (B, T, 40)
  d_layer_2_all = tf.layers.dense(d_layer_1_all, 40, activation=tf.nn.sigmoid, name='f2_att', reuse=tf.AUTO_REUSE)
  # (B, T, 1)
  d_layer_3_all = tf.layers.dense(d_layer_2_all, 1, activation=None, name='f3_att', reuse=tf.AUTO_REUSE)
  # (B, 1, T)
  # 每一个样本都是 [1,T] 的维度，和原始特征的维度一样，但是这时候每个item已经是特征中的一个item和目标item混在一起的数值了
  d_layer_3_all = tf.reshape(d_layer_3_all, [-1, 1, tf.shape(keys)[1]])
  outputs = d_layer_3_all
  # Mask，每一行都有T个数字，keys_length长度为B，假设第1 2个数字是5,6，那么key_masks第1 2行的前5 6个数字为True
  key_masks = tf.sequence_mask(keys_length, tf.shape(keys)[1])   # [B, T]
  key_masks = tf.expand_dims(key_masks, 1) # [B, 1, T]
  # 创建一个和outputs的shape保持一致的变量，值全为1，再乘以(-2 ** 32 + 1)，所以每个值都是(-2 ** 32 + 1)
  paddings = tf.ones_like(outputs) * (-2 ** 32 + 1)
  outputs = tf.where(key_masks, outputs, paddings)  # [B, 1, T]
  # Scale
  outputs = outputs / (keys.get_shape().as_list()[-1] ** 0.5) # T，根据特征数目来做拉伸
  # Activation
  outputs = tf.nn.softmax(outputs)  # [B, 1, T]
  # Weighted sum
  outputs = tf.matmul(outputs, keys)  # [B, 1, H]
  return outputs

残差单元 Residual Unit

避免网络太深而梯度消失。如果某一层的输出已经较好的拟合了期望结果，那么之后的层会被短链而跳过。

输入过两层MLP之后再和原输入进行按位加操作。

def Residual_Unit(input, in_channel, out_channel, stride=1):
    """
    :param input: The input of the Residual_Unit. Should be a 4D array like (batch_num, img_len, img_len, channel_num)
    :param in_channel: The 4-th dimension (channel number) of input matrix. For example, in_channel=3 means the input contains 3 channels.
    :param out_channel: The 4-th dimension (channel number) of output matrix. For example, out_channel=5 means the output contains 5 channels (feature maps).
    :param stride: Integer. The number of pixels to move between 2 neighboring receptive fields.
    """

    # initialize as the input (identity) data
    shortcut = input
    shortcut = Conv2D(out_channel, (1, 1), padding='same', strides=stride)(shortcut)

    # RestNet module
    x = BatchNormalization()(input)
    x = Activation('relu')(x)
    x = Conv2D(in_channel, (1, 1))(x)

    x = BatchNormalization()(x)
    x = Activation('relu')(x)
    x = Conv2D(in_channel, (3, 3), padding='same', strides=stride)(x)

    x = BatchNormalization()(x)
    x = Activation('relu')(x)
    x = Conv2D(out_channel, (1, 1), padding='same')(x)

    # identity
    x = Add()([x, shortcut])

    return x

Cross Layer

交叉网络层是DCN模型中出现一种层。

def cross_layer(x0, x, name):
  with tf.variable_scope(name):
    input_dim = x0.get_shape().as_list()[1]
    w = tf.get_variable("weight", [input_dim], initializer=tf.truncated_normal_initializer(stddev=0.01))
    b = tf.get_variable("bias", [input_dim], initializer=tf.truncated_normal_initializer(stddev=0.01))
    xb = tf.tensordot(tf.reshape(x, [-1, 1, input_dim]), w, 1)
    return x0 * xb + b + x

神经网络实现

一个最简单的神经网络实现

下面是一个极度简化的神经网络实现，没有隐含层，输入是长度为3的数组，输出是一个整数。训练样本数据有四套。

激活函数使用sigmoid。要训练的模型是sigmoid(np.dot(l0,syn0))，其中l0是输入层数据，syn0是要训练的参数。

import numpy as np

# The simplest nerual network
# : No hidden layer

# sigmoid function
# True: f(x) = 1/(1+e^(-x))
# False: f'(x) = f(x)(1-f(x))
def sigmoid(x,deriv=False):
    if(deriv==True): # derivative function: y*(1-y)
        return x*(1-x)
    else:   # origin function
        return 1/(1+np.exp(-x))

# input dataset
X = np.array([  [0,0,1],
                [0,1,1],
                [1,0,1],
                [1,1,1] ])

# output dataset            
y = np.array([[0,0,1,1]]).T

# seed random numbers to make calculation
# deterministic (just a good practice)
np.random.seed(1)

# initialize weights - randomly with mean 0
syn0 = 2*np.random.random((3,1)) - 1

for iter in xrange(10000):
    # forward propagation
    l0 = X
    l1 = sigmoid( np.dot(l0, syn0) ) # model

    # # backward propagation
    # how much did we miss?
    l1_error = y - l1

    # multiply how much we missed by the
    # slope of the sigmoid at the values in l1
    l1_delta = l1_error * sigmoid(l1, True)

    # update weights
    syn0 += np.dot(l0.T, l1_delta)


print "Output After Training:"
print l1
print "Weights after Training:"
print syn0

算法的关键在于，在10000次迭代中，如何更新权值参数，也就是for循环中最后三行代码。

为什么要用 “误差 * 斜率” 来更新权值参数？这就是梯度下降吧。

具有隐藏层的简单神经网络实现

很多场景下，直接输入数据和输出结果是没有直观联系的，联系或者是局部的、或者是间接的，这时候我们可以加入隐藏层来发现和记录这些间接规律。

下面这一个带了一层hidden layer的神经网络。 l0是输入层，样本数据是长度为3的数组（1X3）。 l1是隐含层，运算参数syn0是3X4矩阵。 l2是输出层，运算参数syn1是4X1的矩阵，输出结果是一个整数。

在反向传播计算误差时，某一层的误差是用后一层的”误差 * 斜率”来算的。

import numpy as np

# Simplest nerual network
# one hidden layer

# sigmoid function
# True: f(x) = 1/(1+e^(-x))
# False: f'(x) = f(x)(1-f(x))
def sigmoid(x,deriv=False):
    if(deriv==True): # derivative function: y*(1-y)
        return x*(1-x)
    else:   # origin function
        return 1/(1+np.exp(-x))

X = np.array([[0,0,1],
            [0,1,1],
            [1,0,1],
            [1,1,1]])

y = np.array([[0],
            [1],
            [1],
            [0]])

np.random.seed(1)

# randomly initialize our weights with mean 0
syn0 = 2*np.random.random((3,4)) - 1
syn1 = 2*np.random.random((4,1)) - 1

for j in xrange(60000):

    # Feed forward through layers 0, 1, and 2
    l0 = X  # layer 0 - input
    l1 = sigmoid(np.dot(l0,syn0)) # layer 1 - hidden layer with syn0
    l2 = sigmoid(np.dot(l1,syn1)) # layer 2 - output with syn1

    # how much did we miss the target value?
    l2_error = y - l2

    if (j% 10000) == 0:
        print "Error:" + str(np.mean(np.abs(l2_error)))

    # in what direction is the target value?
    # were we really sure? if so, don't change too much.
    l2_delta = l2_error * sigmoid(l2,deriv=True)

    # how much did each l1 value contribute to the l2 error (according to the weights)?
    l1_error = l2_delta.dot(syn1.T)

    # in what direction is the target l1?
    # were we really sure? if so, don't change too much.
    l1_delta = l1_error * sigmoid(l1,deriv=True)

    syn1 += l1.T.dot(l2_delta)
    syn0 += l0.T.dot(l1_delta)

print
print "Weights after Training:"
print syn0
print syn1
print "Output After Training:"
print l2